Contents

Cálculo de parâmetros de um motor a jacto

Este script calcula os principais parâmetros (temperaturas, pressões, velocidades, empuxo e consumo específico) de um motor a jacto idealizado. As descrições de cada etapa de cálculo estão organizadas em secções.

clc
close all
clearvars

1) Definição dos parâmetros e constantes

RP = 3;
mdot_ar = 2.0;
T3_C = 990;
AF_racio = 71.3;
V1_kmh = 540;
Ta_C = 25;
P1_bar = 1;
eta_c = 0.75;
eta_t = 0.85;
gamma_frio = 1.4;
gamma_quente = 1.333;
R = 287;

2) Conversão de unidades e cálculo de calores específicos

T3 = T3_C + 273.15;       % Conversão de ºC para K
cp_frio = (gamma_frio * R) / (gamma_frio - 1);
cp_quente = (gamma_quente * R) / (gamma_quente - 1);

3) Condições na entrada do motor (Ram Effect)

V1 = V1_kmh * 1000 / 3600;  % km/h para m/s
Ta = Ta_C + 273.15;         % ºC para K
Pa = P1_bar * 1e5;          % bar para Pa
T1 = Ta + (V1^2 / (2 * cp_frio));
P1 = Pa * (T1 / Ta)^(gamma_frio / (gamma_frio - 1));

4) Cálculo de P2, T2 isentrópico e T2 real

P2 = P1 * RP;
T2s = T1 * (P2 / P1)^((gamma_frio - 1) / gamma_frio);
T2 = T1 + (T2s - T1) / eta_c;
V2 = sqrt(V1^2 + 2 * cp_frio * (T2 - T1));

5) Cálculo das entalpias h1 e h2

As entalpias são dadas por: h1r = cp_frio * T1 h2r = cp_frio * T2 Não se adiciona a componente cinética neste termo (meia velocidade ao quadrado), pois é tratada separadamente.

h1r = cp_frio * T1;
h2r = cp_frio * T2;

6) Balanço energético do compressor

O trabalho consumido pelo compressor é: W_dot_c = - (mdot_ar * (h1r - h2r)) Sinal negativo indica que o sistema (ar) recebe trabalho do exterior.

W_dot_c = -(mdot_ar * (h1r - h2r));

7) Pressão na câmara de combustão

Admite-se perda de carga desprezável na câmara de combustão. Logo: P3 = P2

P3 = P2;

8) Balanço energético na turbina

A turbina fornece o trabalho necessário ao compressor (em regime estacionário): W_dot_t = W_dot_c A temperatura de saída T4 resulta da subtracção do trabalho específico transformado em variação de entalpia. Calcula-se também T4s (isentropicamente) e a pressão P4.

W_dot_t = W_dot_c;
T4 = T3 - W_dot_t / (mdot_ar * cp_quente);
T4s = T3 + (T4 - T3) / eta_t;
P4 = P3 * (T4s / T3)^(gamma_quente / (gamma_quente - 1));

9) Nozzle (expansão até pressão ambiente)

Expansão dos gases de P4 até Pa. A temperatura final T5 é calculada isentropicamente: T5 = T4 * (P5 / P4)^((gamma_quente - 1)/gamma_quente) A velocidade de saída V5 é obtida pela diferença de entalpia convertida em energia cinética.

V4 = 0;      % Supondo velocidade nula à saída da turbina (para simplificar)
P5 = Pa;
T5 = T4 * (P5 / P4)^((gamma_quente - 1) / gamma_quente);
V5 = sqrt(V4^2 + 2 * cp_quente * (T4 - T5));

10) Áreas de entrada e de saída

rho1 = Pa / (R * Ta);
A1 = mdot_ar / (rho1 * V1);
rho_5 = P5 / (R * T5);
A5 = mdot_ar / (rho_5 * V5);

11) Empuxo (Thrust)

Thrust = mdot_ar * (V5 - V1)

Thrust = mdot_ar * (V5 - V1);

12) Consumo Específico de Combustível (TSFC)

mdot_combustivel = mdot_ar / AF_racio
TSFC = mdot_combustivel / Thrust

mdot_combustivel = mdot_ar / AF_racio;
TSFC = mdot_combustivel / Thrust;

13) Apresentação dos resultados

Os principais resultados são mostrados no Command Window.

fprintf('Temperatura estática à saída do nozzle (T5): %.2f K\n', T5);
fprintf('Velocidade do jacto à saída do nozzle (V5): %.2f m/s\n', V5);
fprintf('Área de entrada do motor (A1): %.4f m²\n', A1);
fprintf('Área de saída do motor (A5): %.4f m²\n', A5);
fprintf('Empuxo (Thrust): %.2f N\n', Thrust);
fprintf('Consumo específico de combustível (TSFC): %.2e kg/(N·s)\n', TSFC);

Temperatura estática à saída do nozzle (T5): 949.24 K
Velocidade do jacto à saída do nozzle (V5): 644.77 m/s
Área de entrada do motor (A1): 0.0114 m²
Área de saída do motor (A5): 0.0085 m²
Empuxo (Thrust): 989.55 N
Consumo específico de combustível (TSFC): 2.83e-05 kg/(N·s)

14) Gráficos em 4 subplots

1. Variação de Temperatura: T1, T2, T3, T4, T5 2. Variação de Pressão: P1, P2, P3, P4, P5 3. Variação de Velocidades: V1, V2, V4, V5 4. Empuxo (Thrust), representado como uma barra única

T_array = [T1, T2, T3, T4, T5];
P_array = [P1, P2, P3, P4, P5];
Velocidades = [V1, V2, V4, V5];

figure('Name','Parâmetros Principais do Motor a Jacto','NumberTitle','off');

% Subplot 1: Temperatura
subplot(2,2,1)
plot(1:5, T_array, '-o','LineWidth',1.5,'MarkerSize',6)
title('Variação de Temperatura')
xlabel('Estados do escoamento')
ylabel('Temperatura [K]')
xticks(1:5)
grid on

% Subplot 2: Pressão
subplot(2,2,2)
plot(1:5, P_array, '-o','LineWidth',1.5,'MarkerSize',6)
title('Variação de Pressão')
xlabel('Estados do escoamento')
ylabel('Pressão [Pa]')
xticks(1:5)
grid on

% Subplot 3: Velocidade
subplot(2,2,3)
plot(1:length(Velocidades), Velocidades, '-s','LineWidth',1.5,'MarkerSize',6)
title('Variação de Velocidade')
xlabel('Pontos de velocidade')
ylabel('Velocidade [m/s]')
xticks(1:4)
xticklabels({'V1','V2','V4','V5'})
grid on


sgtitle('Resultados Principais do Motor a Jacto')

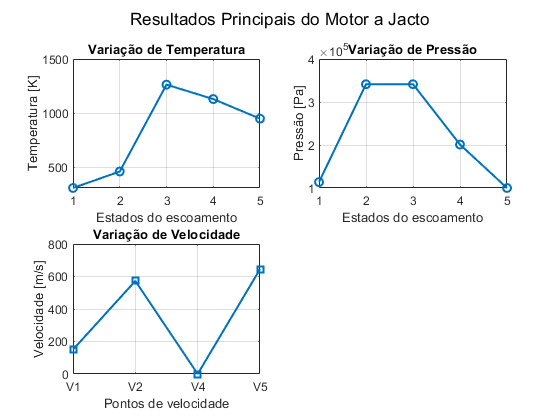
Observa-se que a temperatura alcança o seu valor máximo na câmara de combustão (T3) e diminui ao passar pela turbina (T4), enquanto a pressão é elevada pelo compressor (P2) e depois reduzida até próximo da pressão ambiente no nozzle (P5). Nas velocidades, nota-se que o escoamento acelera significativamente até à saída (V5). Finalmente, o empuxo (Thrust) quantifica a força de propulsão gerada pelo motor.

Published with MATLAB® R2024b